In this discussion, we will explore the fundamental mathematical operations of addition, subtraction, multiplication, and division. These operations form the basis of all mathematical concepts and are crucial for a strong foundation in mathematics.
Addition and Subtraction
Addition
- Symbol: +
- Result: Sum
- Description: Addition involves combining or increasing values. When we add, we are bringing things together.




Subtraction
- Symbol: −
- Result: Difference
- Description: Subtraction involves taking away or decreasing values. It represents the removal or deduction of quantity.




Key Points:
- Addition and subtraction are opposite operations.
- The symbol for addition is ++, and for subtraction, it is −−.
- The result of an addition problem is called the sum, while the result of a subtraction problem is called the difference.
Visualization:
- A number line can be a helpful tool to visualize addition and subtraction. Moving to the right represents addition, and moving to the left represents subtraction.
Example Scenario:
- Selling bags of popcorn where addition represents replenishing stock, and subtraction represents sales.
Multiplication and Division
Multiplication
- Symbol: ×
- Result: Product
- Description: Multiplication is a way of representing repeated addition. It involves combining multiple groups of a certain value.
Division
- Symbol: ÷
- Result: Quotient
- Description: Division is the opposite of multiplication. It involves dividing a large group into smaller subgroups.

Key Points:
- Multiplication and division are also opposite operations.
- The symbol for multiplication is ××, and for division, it is ÷÷.
- The result of a multiplication problem is called the product, and for division, it is called the quotient.
Visualization:
- Multiplication is a convenient way to represent repeated addition. It allows us to calculate the total of multiple groups efficiently.
Understand BODMAS/PEDMAS for Addition Subtraction Multiplication and Division
BODMAS and PEDMAS are acronyms that represent the order of operations in mathematics, guiding the sequence in which different mathematical operations should be performed to solve an expression.
The purpose of these rules is to ensure consistency in mathematical calculations and to avoid ambiguity.
Both acronyms convey the same concept, but their letters may differ depending on the educational system or region. Here’s an explanation of both:
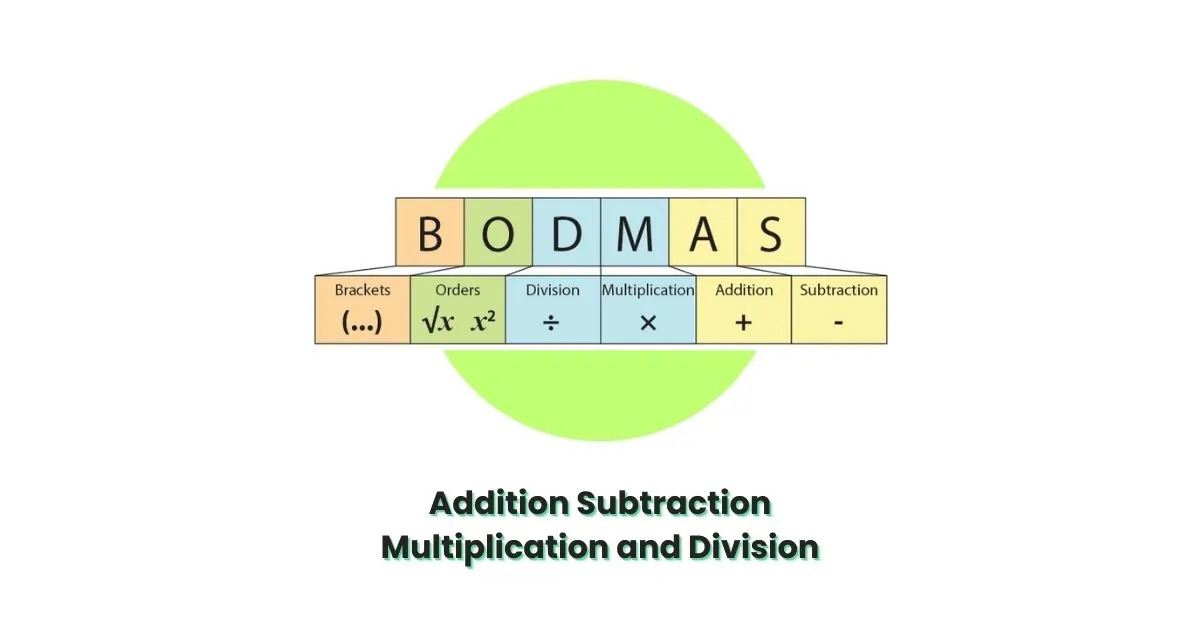
BODMAS
- B: Brackets
- O: Orders (i.e., powers and roots, such as square roots or cubes)
- D: Division
- M: Multiplication
- A: Addition
- S: Subtraction
According to BODMAS, calculations should be performed in the order of brackets, followed by orders, then division and multiplication (from left to right), and finally addition and subtraction (from left to right).
PEDMAS
- P: Parentheses (Brackets)
- E: Exponents (Orders)
- D: Division
- M: Multiplication
- A: Addition
- S: Subtraction
PEDMAS follows the same order of operations as BODMAS but uses the term “parentheses” instead of “brackets.” This is commonly used in the United States and some other regions.
In practice, both BODMAS and PEDMAS serve as mnemonics to help students remember the correct sequence of operations.
When solving mathematical expressions, it’s crucial to follow these rules to obtain consistent and accurate results.
BODMAS or PEDMAS Rules
| Order | Operation | Examples |
|---|---|---|
| 1 | Parentheses or Brackets | ( ), { }, [ ] |
| 2 | Orders (powers and square roots, etc.) | √x, x², x³ |
| 3 | Division and Multiplication (from left to right) | ÷, × |
| 4 | Addition and Subtraction (from left to right) | +, – |
Key Points:
- Work within parentheses or brackets first.
- Evaluate exponents (powers and square roots) next.
- Perform division and multiplication from left to right.
- Perform addition and subtraction from left to right.
Example:
Solve: 3 + 4 × 2 ÷ (5 – 1)
- Parentheses:
(5 – 1) = 4 - Multiplication and Division (left to right):
4 × 2 ÷ 4 = 8÷4=2
8÷4×2=2×2=4 - Addition: 3 + 2 = 5
100+ Addition Subtraction Multiplication and Division Question Worksheet
Easy Questions
$2 + 3 \times 4$
$8 \div 2 + 5$
$6 – 2 \times 3$
$10 \div (2 + 3)$
$4 \times (5 + 2)$
$9 + 2 \div 3$
$(7 – 3) \times 2$
$15 \div (3 + 2)$
$4 + 6 \div 2$
$(8 – 2) \times 4$
$12 \div 3 + 2$
$5 \times (2 + 1)$
$7 + 4 \div 2$
$(6 – 2) \times 5$
$18 \div (3 + 1)$
$3 + 5 \times 2$
$9 \div (3 + 1)$
$(4 – 1) \times 2$
$10 \times 2 \div 5$
$(15 – 3) \div 4$
Medium Questions
$3 + 4 \times 2 – 5$
$10 \div 2 + 6 \times 3$
$8 – 2 \times (7 – 3)$
$15 \div (3 + 2) \times 4$
$(6 + 2) \times (4 – 1)$
$9 + 2 \times (7 – 4) \div 2$
$(5 \times 2) – (8 \div 2)$
$12 \div (3 + 2) + 7 \times 2$
$4 \times (9 – 2) \div 3$
$(14 – 3) \div 2 + 5 \times 2$
$2 \times (4 + 3) – 6$
$9 + 2 \div (4 – 1) \times 5$
$(6 – 2) \times 3 + 7$
$15 \div 3 + 2 \times (8 – 4)$
$4 \times (5 + 2) – 8 \div 2$
$10 \div 2 \times (3 + 1) – 5$
$(7 + 2) \times 4 – 3 \div 2$
$12 \times 2 \div (6 – 2) + 5$
$(9 – 3) \times 2 + 4 \div 2$
$8 + 6 \div (2 \times 3) \times 4$
Hard Questions
$2^3 + 5 \times (12 – 4) \div 2$
$(6 + 2)^2 – 3 \times (4 + 1)$
$18 \div (3 + 1) \times (5 – 2)^2$
$4 \times (9 – 3)^2 \div (2 + 1)$
$(7 – 2) \times 3^2 + 4 \div 2$
$10 \div 2 + 3^2 \times (8 – 4)$
$(5^2 + 2) \times 3 – 4 \div (6 – 2)$
$12 \div (2 \times 3) \times (5 + 3)^2 – 7$
$4^2 \times (6 – 1) + 9 \div (3 + 2)$
$(11 – 3)^2 \div (2 \times 5) + 6$
$3 \times (2^3 + 1) – 5^2 \div 2$
$(8 – 2)^2 \times 4 + 6 \div 3$
$7^2 + 4 \times (9 – 2) \div 5$
$(15 \div 3)^2 \times (4 – 1) + 2$
$6 \times (4^2 – 3) + 2^3 \div 2$
$(10 \div 2)^2 + 5 \times (3 – 1)$
$9 + 2^3 \div (4 – 1) \times 5$
$4 \times (6^2 \div 3) – 2 + 7$
$(9 – 2)^2 \times 3 + 4 \div 2$
$8 + 6 \div (2 \times 3)^2 \times 4$
Very Hard Questions
$2^{(3^2)} + 5 \times (12 – 4) \div 2 – 3$
$(6 + 2)^3 – 3 \times (4 + 1)^2 + 7$
$\sqrt{18 \div (3 + 1)} \times (5 – 2)^2 + 1$
$4 \times (9 – 3)^2 \div (2 + 1)^2 – 5$
$(7 – 2) \times (3^2 + 1) – 4 \div 2 + 6$
$10 \div 2 + 3^2 \times (8 – 4) \div 2$
$(5^2 + 2)^2 \times 3 – 4 \div (6 – 2)^2 + 1$
$12 \div (2 \times 3) \times (5 + 3)^2 – 7^2 + 2$
$4^2 \times (6 – 1) + 9 \div (3 + 2)^2 – 3$
$(11 – 3)^2 \div (2 \times 5) + 6 \times 2^3 – 1$
Certainly! Here are 10 even more complex BODMAS (Order of Operations) problems:
$2^{(3^2)} + 5 \times (12 – 4) \div 2 – \sqrt{3^3} + 7$
$(6 + 2)^3 – \sqrt{3 \times (4 + 1)^2} + 7^2 \div 2$
$\sqrt{18 \div (3 + 1)} \times (5 – 2)^2 + \frac{1}{2} \times (4^2 – 1)$
$4 \times (9 – 3)^2 \div (2 + 1)^2 – 5^{\frac{1}{2}} + 3$
$(7 – 2) \times (3^2 + 1) – 4 \div 2 + 6^2 \div \sqrt{3}$
$10 \div 2 + 3^2 \times (8 – 4) \div 2 + \sqrt{81}$
$(5^2 + 2)^2 \times 3 – \frac{4}{(6 – 2)^2} + 1$
$12 \div (2 \times 3) \times (5 + 3)^2 – 7^2 + 2 \times 3^{(1/2)}$
$4^2 \times (6 – 1) + 9 \div (3 + 2)^2 – \sqrt{3^2}$
$(11 – 3)^2 \div (2 \times 5) + 6 \times 2^3 – \frac{1}{2} \times 3^2$

Leave a Reply