Introduction
Have you ever looked at a graph and puzzled how steep a line is or how speedy a amount is converting over time? Understanding the way to find the slope is a fundamental talent in arithmetic and plays a vital position in numerous fields inclusive of physics, engineering, economics, and extra. Whether you are a pupil struggling with algebra or a professional looking to refresh your math capabilities, this complete guide will stroll you through everything you need to understand about how to find slope.
1: What is Slope? (How to find slope)
Before diving into the intricacies of finding slope, permits begin with the fundamentals. What exactly is a slope, and why is it so crucial?
1.1 Definition of Slope
In easy terms, slope measures the steepness of a line on a graph. It tells us how one variable (commonly represented on the y-axis) changes regarding another variable (commonly represented on the x-axis). The method for calculating slope, often denoted as ‘m,’ is:
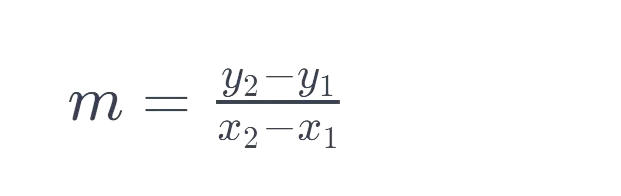
Example: Suppose we have two points on a line: (1, 3) and (4, 9). To find the slope, we use the formula:
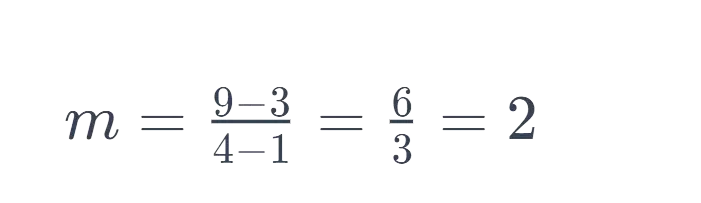
So, the slope of the line passing through these two points is 2.
1.2 Importance of Slope
Slope isn’t always only a mathematical idea limited to textbooks; it has actual-international applications:
- Geometry: Slope helps define the attitude at which strains intersect.
- Physics: Slope is critical in reading movement, acceleration, and velocity.
- Economics: Economists use slope to investigate deliver and call for curves.
- Engineering: Engineers use slope to design roads, bridges, and greater.
- Environmental Science: Slope is critical in knowledge terrain and panorama features.
2: Different Forms of Slope
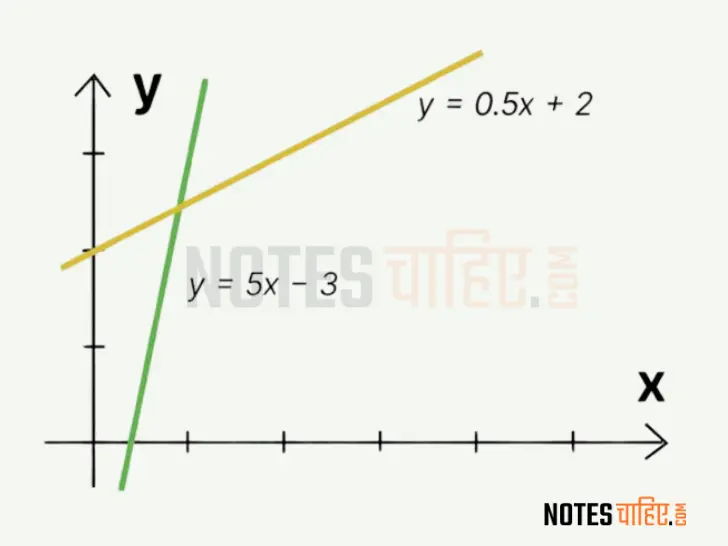
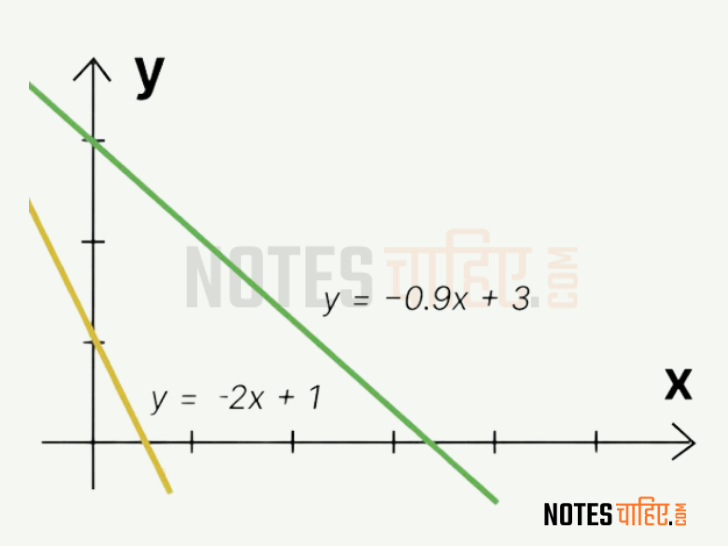
2.1 Positive and Negative Slope
A Positive slope indicates that as the x-values increase, the y-values also increase. A negative slope approach that because the x-values increase, the y-values decrease.
Example: Imagine a line with a positive slope: as time (x) increases, the temperature (y) also increases. Conversely, a negative slope would indicate that as time increases, temperature decreases.
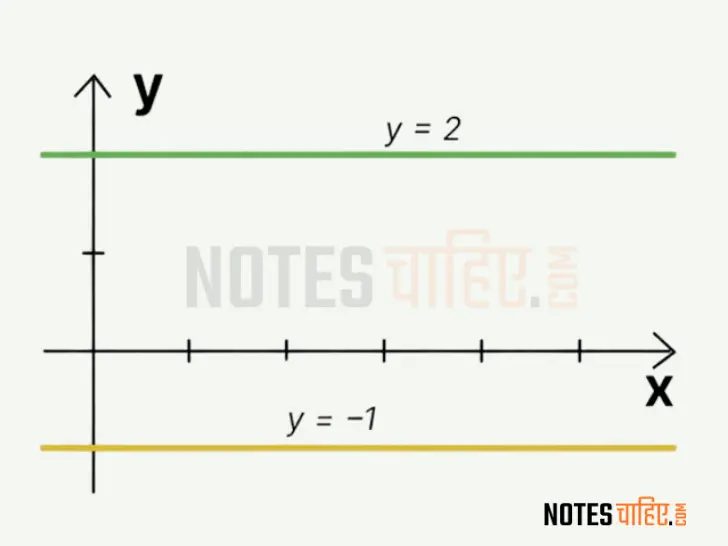
2.2 Zero and Undefined Slope
A zero slope indicates that the line is horizontal, meaning there’s no exchange inside the y-values as x-values change. An undefined slope takes place whilst the road is vertical, indicating that there’s no change within the x-values as y-values exchange.
Example: A road with a zero slope would be completely flat, with no incline. An undefined slope in a building blueprint suggests a vertical wall.
Best Notes Making Format, Ideas And Examples 2023
2.3 Three Slopes as a Rate of Change
Slope can represent rates of change, such as speed, growth, or decline.
Example: In finance, if the slope of a stock price graph is positive, it means the stock is gaining value over time. A negative slope indicates a decline in value.
3: Finding Slope from Graphs
3.1 Using the Rise-over-Run Method
To find the slope between two points, you can use the rise-over-run method.
Example: Consider points A(2, 4) and B(6, 10). The rise is 10 – 4 = 6, and the run is 6 – 2 = 4. So, the slope is
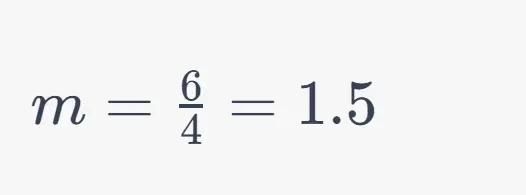
3.2 Slope of a Curve
Finding the slope of a curve can be more complicated. We’ll discuss how to locate the slope of a curve at a specific point, referred to as the on-the-spot slope or derivative
Example: For the curve y = x^2, to find the slope at the point (2, 4), you’d take the derivative, which is dy/dx = 2x. Plug in x = 2, and you get a slope of 4.
4. Finding Slope from a Graph
While finding the slope of a line from the graph, one method is to directly apply the formula given the coordinates of two points lying on the line. Let’s say the values of the coordinates of the two points are not given. So, we have another method as well to find the slope of the line. In this method, we try to find the triangle of angels made by the line with the x-axis. Hence, we find the slope as given below.

The slope of a line is a unique and constant value. Therefore, the slopes determined using Methods 1 and 2 will be identical. Furthermore, if we are provided with the equation of a straight line, which can be expressed in the general form:
y = mx + b
The slope of the line is represented by ‘m.’ Consequently, ‘m’ determines the slope of any straight line.

5. Finding Slope from Equations
5.1 Slope-Intercept Form (y = mx + b)
This section will delve into the slope-intercept form of an equation and demonstrate how it allows you to quickly identify the slope (m) and the y-intercept (b) in a given context.
5.2 Point-Slope Form (y – y1 = m(x – x1))
When you have a specific point on a line, the point-slope form becomes invaluable. This section will guide you through finding the slope using this form, providing examples for clarity.
6. Slope of Horizontal Line
We understand that a horizontal line is a straight line that runs parallel to the x-axis within a coordinate plane. This means it extends either from left to right or right to left. Consequently, the overall change in the y-coordinates for a horizontal line is zero. Therefore, the slope of a horizontal line (regression line slope) can be expressed as follows:
The slope of a horizontal line, denoted as ‘m,’ equals Δy/Δx, which is unequivocally zero.
7. Slope of Perpendicular Lines
A pair of lines that are perpendicular to each other always forms a 90-degree angle between them. Let’s consider two perpendicular lines, labeled as l1 and l2 on the coordinate plane. These lines make angles θ1 and θ2, respectively, with the x-axis. These angles satisfy the external angle theorem, which means that θ2 = θ1 + 90 degrees.
As a result of this relationship, the slopes of these lines can be expressed as follows:
- The slope of l1 is m1 = tan θ1.
- The slope of l2 is m2 = tan (θ1 + 90 degrees), which can be simplified to m2 = -cot θ1.
Therefore, when we multiply the slopes of two perpendicular lines, we obtain the result -1. In mathematical terms, this relationship can be expressed as m1×m2=−1
Hence, the product of the slopes of two perpendicular lines is always equal to -1.
8: Conclusion
Congratulations! You’ve made it through this complete manual on how to find the slope. Whether you’re a scholar preparing for a math exam or an expert applying these principles for your work, knowledge slope is a precious talent. Remember that practice makes perfect, so don’t hesitate to address extra problems and explore actual-world packages to solidify your understanding. The slope may also look like a simple idea, however, its applications are boundless, making it an essential tool within the global of arithmetic and past.
So, move beforehand and embody the sector of slopes, and you will locate that it is no longer just about numbers; it is approximately expertise in the fundamental relationships that shape our international.


Leave a Reply