Maths Formulas For Class 10: The provided statement introduces a comprehensive list of essential mathematical formulas for CBSE Class 10 students, covering topics like Real Numbers, Polynomials, Trigonometry, and more.
This compilation serves as a valuable revision checklist for the upcoming 2024 board exam.
The list includes not only formulas but also important terms and properties, enhancing students’ understanding.
Using this resource for revision aids in reinforcing knowledge and preparing students thoroughly for the exam, emphasizing the significance of regular practice and practical application of these mathematical concepts.
Maths Formulas For Class 10 Revise For Board 2024




PDF covers Complete Concepts and Formulae for following:
Unit I: Number Systems
- Chapter 1: Real Numbers
- Chapter 2: Polynomials
Unit II: Algebra
- Chapter 3: Pair of Linear Equations in Two Variables
- Chapter 4: Quadratic Equations
- Chapter 5: Arithmetic Progressions
Unit III: Coordinate Geometry
- Chapter 6: Coordinate Geometry
Unit IV: Geometry
- Chapter 7: Triangles
Unit V: Trigonometry
- Chapter 8: Introduction to Trigonometry
- Chapter 9: Some Applications of Trigonometry
Unit VI: Mensuration
- Chapter 10: Circles
- Chapter 11: Areas Related to Circles
- Chapter 12: Surface Areas and Volumes
Unit VII: Statistics and Probability
- Chapter 13: Statistics
- Chapter 14: Probability
Ch1: Real Numbers
Real Numbers(R)
|
____________|____________
| |
Rational Numbers(Q) Irrational Numbers
| |
P/Q Form (Fractional) Non-Terminating, Non-Repeating Decimals
| (Ex. √2, e, π, 1.2345678910111213.. )
________|__________________________
| | |
Terminating Non-Terminating, Integers (Z)
Decimals Repeating Decimals (...-3,-2,-1,0,1,2,3,...)
(Ex. 0.5, 2.5, 0.3333..., |
2.123123) |
_______________|_____________
| |
Whole Numbers (W) Natural Number (N)
(0,1,2,3...) (1,2,3,4...) Natural Numbers (N): ${1, 2, 3, 4, 5,…}
Whole Numbers (W): ${0, 1, 2, 3, 4, 5,…}
Integer Number (Z)= {…,−3,−2,−1,0,1,2,3,…}
Rational Numbers: p/q form where p and q are integer
LCM(a,b) x HCF(a,b) = a⋅b
LCM (P, Q, R):
$\frac{{P \cdot Q \cdot R}}{{\text{{HCF}}(P, Q) \cdot \text{{HCF}}(Q, R) \cdot \text{{HCF}}(P, R)}}$
HCF (P, Q, R):
$\frac{{P \cdot Q \cdot R}}{{\text{{LCM}}(P, Q) \cdot \text{{LCM}}(Q, R) \cdot \text{{LCM}}(P, R)}}$
Chapter 2: Polynomials
$(a+b)^2 = a^2 + 2ab + b^2$
$(a-b)^2 = a^2 – 2ab + b^2$
$(x+a)(x+b) = x^2 + (a+b)x + ab$
$a^2 – b^2 = (a+b)(a-b)$
$a^3 – b^3 = (a-b)(a^2 + ab + b^2)$
$a^3 + b^3 = (a+b)(a^2 – ab + b^2)$
$(a+b)^3 = a^3 + 3a^2b + 3ab^2 + b^3$
$(a-b)^3 = a^3 – 3a^2b + 3ab^2 – b^3$
Chapter 3: Pair of Linear Equations in Two Variables
- Linear equation in one variable: (ax + b = 0)
- Linear equation in two variables: (ax + by + c = 0)
$a_1x + b_1y$ + $c_1 = 0$, $a_2x + b_2y + c_2 = 0$
| Scenario | Condition | Graphical | Example |
|---|---|---|---|
| Unique Solution (One Solution) | a1/a2 ≠ b1/b2 | Lines intersect at a single point | 2x + 3y = 7 and x – y = 1 |
| Infinitely Many Solutions | a1/a2 = b1/b2 = c1/c2 | Lines completely overlap | 3x – 6y = 9 and x – 2y = 3 |
| No Solution | a1/a2 = b1/b2 ≠ c1/c2 | Lines are parallel | 4x + 2y = 8 and 2x + y = 5 |
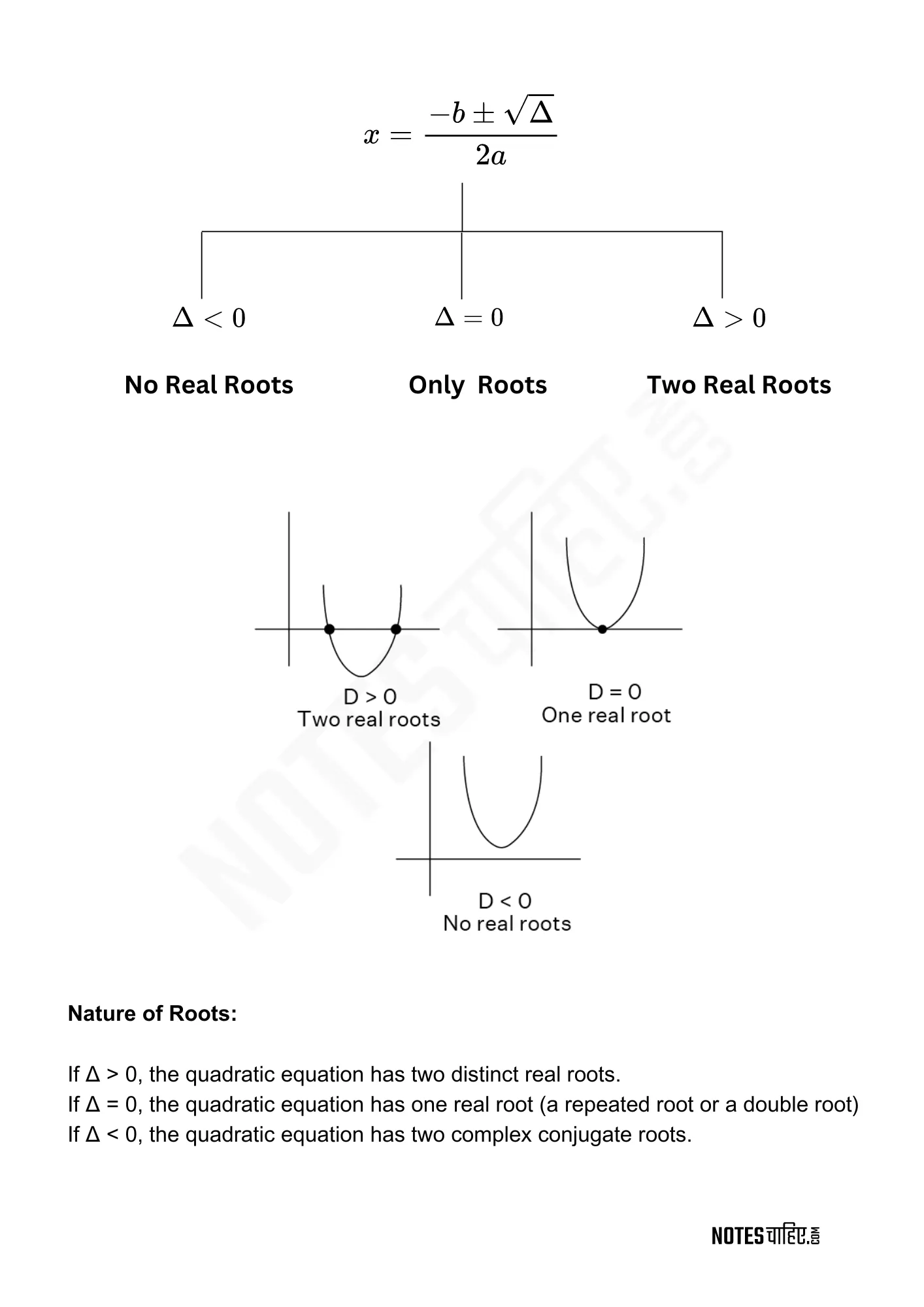
Ch4: Quadratic Equations
- $x = \frac{{-b \pm \sqrt{{b^2 – 4ac}}}}{{2a}}$
- Discriminant: $b^2 – 4ac$
Ch5: Arithmetic Progressions
- (n)th term of AP: a + (n-1)d
- Sum of (n) terms in AP: $S_n = \frac{n}{2}[2a + (n-1)d]$
- Sum of all terms in AP with the last term (l): $\frac{n}{2}(a + l)$
Ch6: Triangles
- Area of Triangle: A = $\frac{1}{2}bh$
- Area of Isosceles Triangle: $\frac{1}{4}b\sqrt{4a^2 – b^2}$
- Area of Right Triangle: A = $\frac{1}{2}\times \text{Base} \times \text{Height}$
- Area of Equilateral Triangle: A = $\frac{\sqrt{3}}{4} \times \text{side}^2$
Ch7: Coordinate Geometry
- Distance Formula: $\sqrt{(x_2 – x_1)^2 + (y_2 – y_1)^2}$
- Section Formula: $\left(\frac{m_1x_2 + m_2x_1}{m_1 + m_2}, \frac{m_1y_2 + m_2y_1}{m_1 + m_2}\right)$
- Mid-point Formula: $\left(\frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}\right)$
Ch8: Introduction to Trigonometry
Basic Trigonometric Ratios:
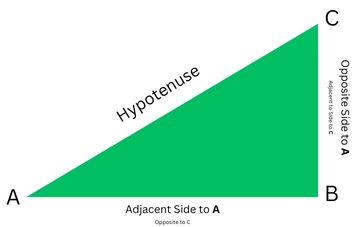
Sine (sin) of an angle A:
$\sin A = \frac{\text{Opposite Side}}{\text{Hypotenuse}}$
Cosine (cos) of an angle A:
$\cos A = \frac{\text{Adjacent Side}}{\text{Hypotenuse}}$
Tangent (tan) of an angle A:
$\tan A = \frac{\text{Opposite Side}}{\text{Adjacent Side}}$
Reciprocal Trigonometric Ratios:
Cosecant (cosec) of an angle A:
$\csc A = \frac{1}{\sin A}$
Secant (sec) of an angle A:
$\sec A = \frac{1}{\cos A}$
Cotangent (cot) of an angle A:
$\cot A = \frac{1}{\tan A}$
Trigonometric Identities:
Pythagorean Identity:
$\sin^2 A + \cos^2 A = 1$
$\csc ^2 A – \cot^2 A = 1$
$\sec^2 A – \tan^2 A = 1$
Reciprocal Identity:
$\csc A = \frac{1}{\sin A}, \quad \sec A = \frac{1}{\cos A}, \quad \cot A = \frac{1}{\tan A}$
Quotient Identity:
$\tan A = \frac{\sin A}{\cos A}$
Complementary Angles:
Complementary Angle Relationship:
$\sin (90^\circ – A) = \cos A, \quad \cos (90^\circ – A) = \sin A, \quad \tan (90^\circ – A) = \cot A$
Trigonometric Ratios for Standard Angles:
Trigonometric Ratios for 0°, 30°, 45°, 60°, 90°:
| Angle | Sine (sin) | Cosine (cos) | Tangent (tan) | Cotangent (cot) |
|---|---|---|---|---|
| 0° | 0 | 1 | 0 | undefined |
| 30° | 1/2 | √3/2 | 1/√3 | √3 |
| 45° | √2/2 | √2/2 | 1 | 1 |
| 60° | √3/2 | 1/2 | √3 | 1/√3 |
| 90° | 1 | 0 | undefined | 0 |
Ch9: Some Applications of Trigonometry
Angle of Elevation and Depression:
- If you are looking up at an object, it’s the angle of elevation.
- If you are looking down at an object, it’s the angle of depression.
Ch10: Circles
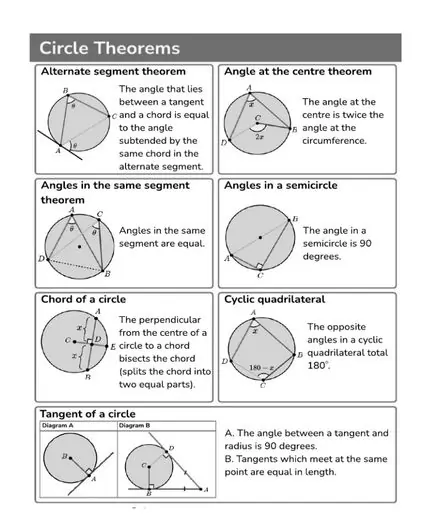
| Theorem | Statement |
|---|---|
| Tangent is Perpendicular to Radius | A tangent to a circle is perpendicular to the radius through the point of contact. |
| Lengths of Tangents from an External Point | The lengths of tangents drawn from an external point to a circle are equal. |
| Angles in the Same Segment | The angles in the same segment of a circle are equal. |
| Angle at the Centre is Twice Angle at the Circumference | The angle subtended by an arc at the center of a circle is twice the angle it subtends at any point on the circumference. |
| Cyclic Quadrilateral | The sum of the opposite angles of a cyclic quadrilateral is 180°. |
| Angles in a Semicircle | An angle in a semicircle is a right angle. |
| Equal Chords Subtend Equal Angles | Equal chords of a circle subtend equal angles at the center. |
| Perpendicular from the Center to a Chord Bisects It | The perpendicular from the center of a circle to a chord bisects the chord. |
| Equal Chords are Equidistant from the Center | Equal chords of a circle are equidistant from the center. |
Ch11: Areas Related to Circles
Circumference of a Circle:
$C = 2\pi r$
Where (C) is the circumference, and (r) is the radius of the circle.
Area of a Circle:
$A = \pi r^2$
Where (A) is the area, and (r) is the radius of the circle.
Area of a Sector:
$A_{\text{sector}} = \frac{n}{360} \pi r^2$
Where (n) is the central angle of the sector in degrees.
Length of an Arc:
$L_{\text{arc}} = \frac{n}{360} \times 2\pi r$
Where (n) is the central angle of the arc in degrees.
Area of a Segment:
$A_{\text{segment}} = A_{\text{sector}} – A_{\text{triangle}}$
Where $A_{\text{sector}}$ is the area of the sector, and $A_{\text{triangle}}$ is the area of the triangle formed by the radii and the chord of the segment.
Ch13: Statistics
Mean for Grouped Data:
- Direct Method: $\bar{x} = \frac{\sum f_i \cdot x_i}{N}$
- Assumed Mean Method: $\bar{x} = A + \frac{\sum f_i \cdot u_i}{N}$
- Step Deviation Method: $\bar{x} = A + \frac{\sum f_i \cdot u_i}{N \cdot h}$
- Where:
- $\bar{x}$ is the mean.
- $f_i$ is the frequency of the $i^{th}$ class.
- $x_i$ is the midpoint of the $i^{th}$ class.
- ( N ) is the total number of observations.
- ( A ) is the assumed mean.
- $u_i$ is the deviation of $x_i$ from A.
- h is the class width.
Mode: The value that occurs most frequently in a data set.
Median: The middle value of a data set when it is ordered.
Mode of Grouped Data:
$\text{Mode} (l) = l + \frac{(f_1 – f_0)}{(2f_1 – f_0 – f_2)} \times h$
where:
l is the lower limit of the modal class
h is the class size
$f_1$ is the frequency of the modal class
$f_0$ is the frequency of the class preceding the modal class
$f_2$ is the frequency of the class succeeding the modal class.
Median for Grouped Data:
$\text{Median} (l) = l + \frac{\frac{n}{2} – cf}{f} \times h$
where:
l is the lower limit of the median class
n is the total number of observations
cf is the cumulative frequency of the class preceding the median class
f is the frequency of the median class
h is the class size.
Ch14: Probability
1. Basic Probability Formula:
P(E) = n(E) / n(S)
- P(E) represents the probability of an event E occurring.
- n(E) represents the number of favorable outcomes for event E.
- n(S) represents the total number of possible outcomes in the sample space.
Example: If you toss a fair coin, the probability of getting heads is 1/2 because there’s 1 favorable outcome (heads) out of 2 possible outcomes (heads or tails).
2. Probability of Not an Event:
P(E’) = 1 – P(E)
- P(E’) represents the probability of the event E not occurring (also called the complementary event).

