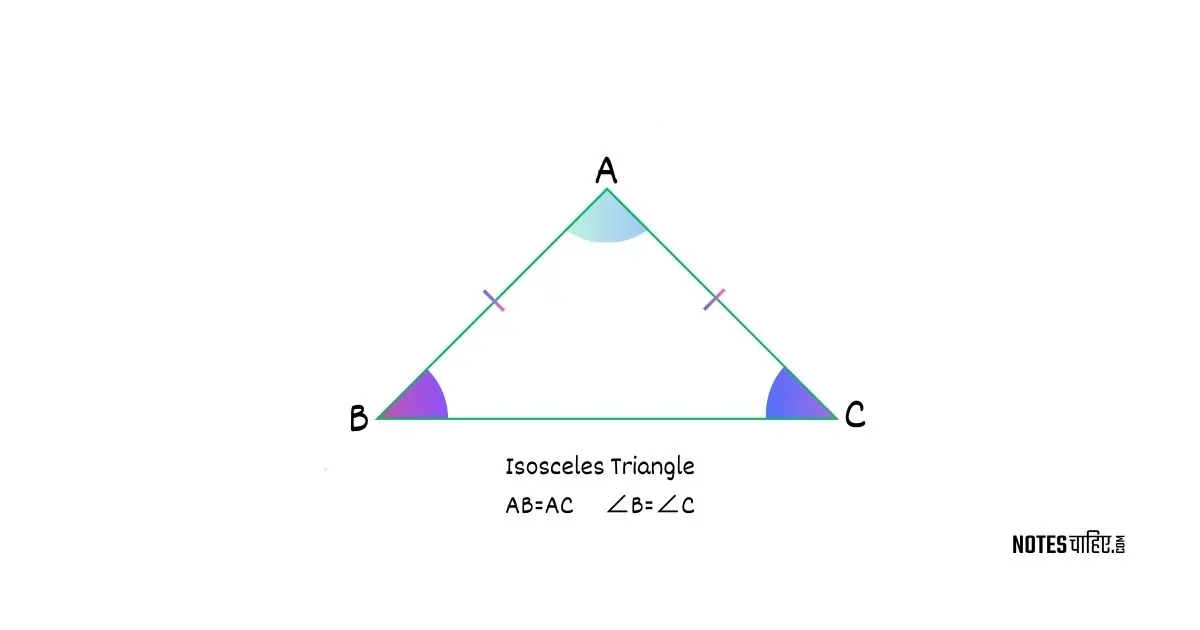
What Is Isosceles Triangle? Properties, Formula, and Problems

An Isosceles Triangle is a specific type of triangle distinguished by the property that it has two sides of equal length. In this geometric configuration, the angles opposite these equal sides are also equal in measure. This distinctive feature sets isosceles triangles apart from other triangle types, such as scalene or equilateral triangles, and leads to various interesting geometric properties.

In this article, we will walk you through the complete about Isosceles Triangle with some practice problems so that you can grab the concepts completely good.

What Is Isosceles Triangle?

An isosceles triangle is a geometric figure that derives its name from its defining characteristic — the presence of two sides of equal length.

The term “isosceles” originates from the Greek words “isos,” meaning “equal,” and “skelos,” meaning “leg.” Thus, an isosceles triangle literally translates to a triangle with equal legs.

Suppose in this triangle △ABC, if sides AB and AC are equal, then △ABC is an isosceles triangle where ∠B = ∠C.

The theorem that describes the isosceles triangle is “if the two sides of a triangle are equal, then the angle opposite to them are also equal”.

Grade Calculator 2024: Check X out Y Points To Grade Online

Properties Of Isosceles Triangle

Property	Explanation
Congruent Sides	Two sides of an isosceles triangle are congruent to each other.
Base Definition	The third side, unequal to the others, is referred to as the base.
Congruent Angles	The angles opposite the congruent sides are themselves congruent.

Isosceles Triangle Theorem

The Isosceles Triangle Theorem is a fundamental geometric principle that establishes a relationship between the sides and angles of an isosceles triangle.

The theorem states that if two sides of a triangle are congruent (of equal length), then the angles opposite those sides are also congruent (equal).

Mathematically, the theorem can be expressed as:

Isosceles Triangle Theorem:

If line AB ≅ AC in triangle ABC, then ∠B ≅ ∠C.

Here’s a breakdown of the components of the theorem:

Isosceles Triangle (△ABC): This is the triangle under consideration, and the theorem specifically focuses on an isosceles triangle, where sides AB and AC are equal.
Congruent Sides: line AB ≅ AC states that the two sides opposite angles A and B (the base angles) are of equal length.
Congruent Angles: ∠B ≅ ∠C asserts that the angles opposite the congruent sides (angles B and C) are also of equal measure.

Visual Representation:

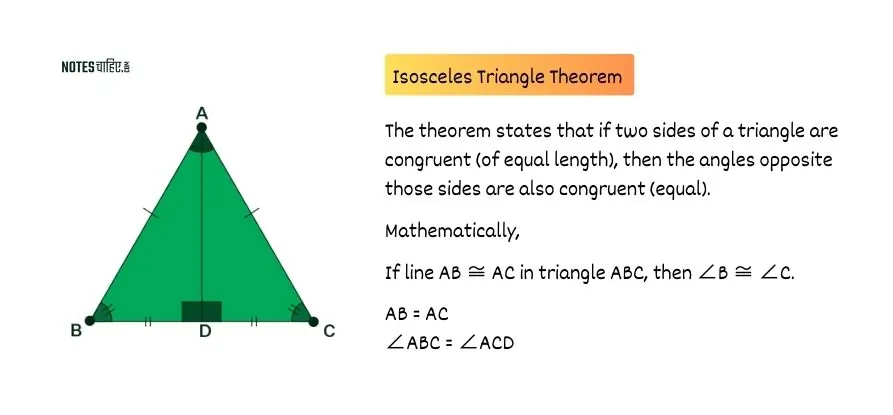
In the diagram, ∠A and ∠B are the base angles, and sides AB and AC are congruent. The Isosceles Triangle Theorem affirms that ∠A and ∠B are equal due to the equality of the corresponding sides.

Types of Isosceles Triangle

In an isosceles triangle, where two sides are of equal length, the relationships between the angles can vary based on different situations. Let’s explore several scenarios:

1. Equal Base Angles:

Situation: Both base angles are equal.
Example: In triangle ABC with sides AB = AC, if ∠A = ∠B, then it’s an isosceles triangle.
Relation: ∠A = ∠B(base angles are congruent).

2. Unequal Base Angles:

Situation: The base angles are not equal.
Example: In triangle XYZ with sides XY = XZ, if ∠X ≠ ∠Y, it’s still an isosceles triangle.
Relation: ∠X ≠∠Y, but sides XY = XZ, making it isosceles.

3. Right Isosceles Triangle:

Situation: One base angle is a right angle (90 degrees).
Example: In triangle PQR with PQ = PR, if ∠Q = 90°, it’s a right isosceles triangle.
Relation: ∠P = ∠R = 45° (base angles are equal).

4. Obtuse Isosceles Triangle:

Situation: One base angle is obtuse (more than 90°).
Example: In triangle LMN with LM = LN, if ∠L > 90°, it’s an obtuse isosceles triangle.
Relation: ∠M = ∠N (base angles are congruent).

5. Acute Isosceles Triangle:

Situation: All angles, including base angles, are acute (less than 90°).
Example: In triangle UVW with UV = UW, if ∠U, ∠V, ∠W are acute, it’s an acute isosceles triangle.
Relation: ∠U = ∠W < 90°(base angles are congruent).

These situations illustrate the versatility of isosceles triangles. While the sides’ equality is a constant, the angles’ relationships can vary, giving rise to different geometric configurations and properties.

Formulas Related to Isosceles Triangles

General Formulas:

Area ((A)):
A = $\frac{1}{2} \times \text{Base} \times \text{Height} $

The area of an isosceles triangle can be calculated using the standard triangle area formula. The height is determined by drawing a perpendicular line from the vertex angle to the base, creating two congruent right-angled triangles.

Perimeter ((P)):
$ P = \text{Side}_1 + \text{Side}_2 + \text{Base} $

The perimeter of an isosceles triangle is the sum of its three sides.

Angle Formulas:

Base Angles (∠B, ∠C):

In an isosceles triangle ABC with sides (AB = AC), the base angles are congruent:
[ ∠B = ∠C]
This symmetry is a key property of isosceles triangles.

Vertex Angle (∠A):

In an isosceles triangle ABC with sides (AB = AC), the vertex angle can be found using the supplementary angle property:
$[ \angle A = 180^\circ – 2 \times \text{Base Angle} ]$
The vertex angle is determined by subtracting twice the measure of one of the base angles from 180 degrees.

Special Cases:

Right Isosceles Triangle:

If $(\angle B = 90^\circ)$, then $(\angle C = 90^\circ)$, and the Pythagorean theorem can be applied:
$[ \text{Hypotenuse}^2 = \text{Leg}^2 + \text{Leg}^2 ]$
This formula is specific to right isosceles triangles and relates the sides using the Pythagorean theorem.

Law of Cosines:

In a general isosceles triangle ABC:
$[ \text{Side}_3^2 = \text{Side}_1^2 + \text{Side}_2^2 – 2 \times \text{Side}_1 \times \text{Side}_2 \times \cos(\angle A) ]$
The law of cosines provides a relationship between the sides and angles of a triangle, including isosceles triangles.

Apollonius Theorem:

In an isosceles triangle ABC, if D is the midpoint of the base BC:
$[ AB^2 + AC^2 = 2(AD^2 + BD^2) ]$
Apollonius theorem relates the sides and medians of an isosceles triangle.

These formulas offer a comprehensive toolkit for understanding and solving problems involving isosceles triangles. Depending on the given information and context, different formulas can be applied to analyze and derive various geometric properties.

10 Solved Problems On Isosceles Triangle

Q1. In an isosceles triangle ABC, if $\angle A = 50^\circ $, what is the measure of ( \angle B )?

Ans:
Since an isosceles triangle has two congruent base angles, $\angle B = \angle C $. Therefore, $\angle B = \angle C = \frac{1}{2} \times (180^\circ – \angle A = 65^\circ $.

Q2. If the base angles of an isosceles triangle are $\angle X = 80^\circ$, what is the measure of the vertex angle $\angle Y$?

Ans:
Since the base angles are congruent, $\angle Y = \angle X = 80^\circ$.

Q3.
In an isosceles triangle ABC with AB = AC = 12cm, and $\angle A = 40^\circ$, find the area of the triangle.

Ans:
Using the formula for the area of a triangle A = $\frac{1}{2} \times \text{Base} \times \text{Height}$, the area is A = $\frac{1}{2} \times 12 \times 12 \times \tan(40^\circ$.

Q4.
If an isosceles triangle has a perimeter of 30 units, and one side is 10 units, what are the lengths of the other two sides?

Ans:
Let the lengths of the congruent sides be ( x ). Since the perimeter is the sum of the three sides, ( 10 + x + x = 30 hence x=10.

Q5.
In an isosceles right triangle, if one leg is 5 cm, what is the length of the hypotenuse?

Ans:
In a right isosceles triangle, the legs are congruent, so the hypotenuse is $\sqrt{2}$ times the length of one leg. Thus, the hypotenuse is $5 \sqrt{2}$cm.

Q6.
If $\angle A$ is the vertex angle of an isosceles triangle ABC, what is the measure of $\angle C $?

Answer:
The base angles are congruent, so $angle C = $\angle B$.

Q7.
In an isosceles triangle, the lengths of the equal sides are 8 cm each. If the vertex angle is $\angle A = 60^\circ$, what is the area of the triangle?

Answer:
Use the formula A = $\frac{1}{2} \times \text{Base} \times \text{Height}$, and find the height using trigonometry.

Q8.
If the base angles of an isosceles triangle are $\angle P = 45^\circ$, what is the measure of the vertex angle $\angle Q$?

Answer:
Since the base angles are congruent, $\angle Q = \angle P = 45^\circ$.

Q9.
In an isosceles triangle, if the base is 16 cm and one base angle is $ \angle X = 30^\circ$, find the length of the equal sides.

Answer:
Use trigonometry to find the length of the equal sides using $\tan(30^\circ) = \frac{\text{Height}}{16}$.

Q10.
In a right isosceles triangle, if the hypotenuse is 10 cm, what is the length of each leg?

Answer:
Since it is a right isosceles triangle, the legs are congruent. Use the Pythagorean theorem to find the length of each leg.