Every student who has taken either Standard or Basic Maths they must have to practice All Theorems and Proves that are asked in Board Exams.
NCERT has theorems from chapter of circle and triangle. But there are many proves from other chapters such as Real Number, Triangle, Introduction to Trigonometry, and Circles.
Here we have covered board exam most repeated BPT theorem to all PYQ proves so that you can get confident on how to solve these problems.
We have researched lot before making this useful All Theorem and Prove PDF Notes. We are providing it for free so please share it to all of your friends.
Download Class 10 All Theorem and Prove PDF Notes Free

Triangle BPT Theorem: Basic Proportionality Theorem (Thales)

The Basic Proportionality Theorem, also known as Thales’ Theorem, is a fundamental concept in geometry. It deals with the relationship between parallel lines and the sides of a triangle they intersect.
Here’s the gist of the theorem:
- Imagine a triangle (ABC) and a line (DE) drawn parallel to one of its sides (BC).
- This line DE intersects the other two sides of the triangle (AB and AC) at distinct points (D and E).
The theorem states that this line divides the two intersected sides (AB and AC) proportionally. In other words:
- The ratio of the lengths AD to DB (AD/DB) is equal to the ratio of the lengths AE to EC (AE/EC).
This basically means that line DE cuts off similar slices of the two sides it intersects, relative to their total lengths.
There are several applications of this theorem, including:
- Finding missing side lengths in triangles
- Proving triangles are similar
- Solving geometric problems involving parallel lines and proportions
Triangle Theorem: Converse of Basic Proportionality Theorem
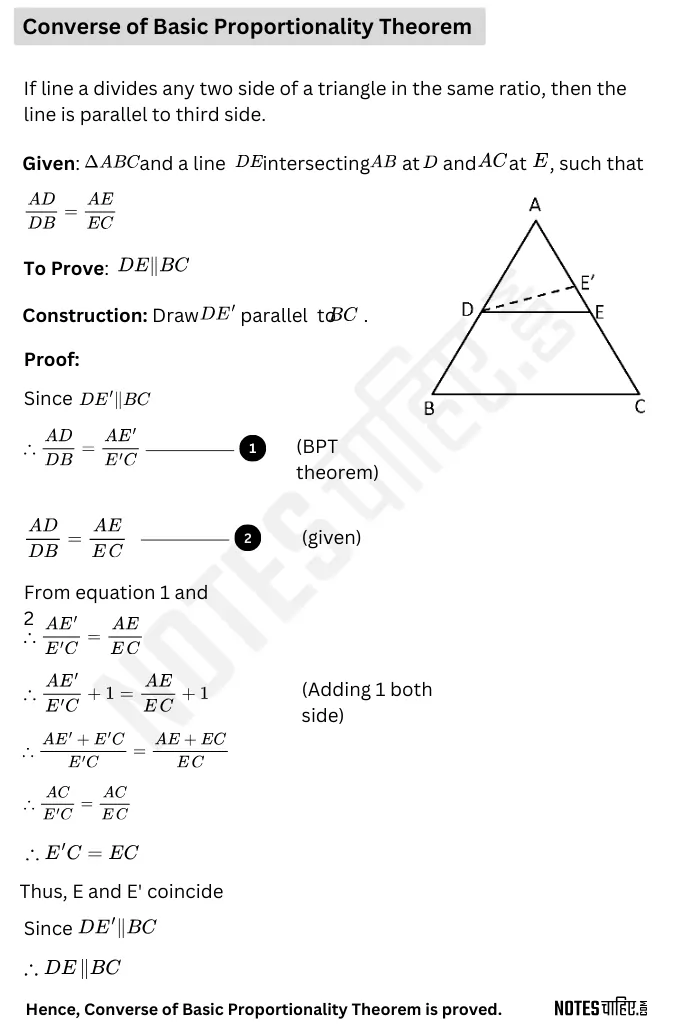
The converse of the Basic Proportionality Theorem (BPT) is another statement about triangles and parallel lines, but it flips the cause and effect relationship.
Here’s the converse:
- Imagine a triangle (ABC) and a line (DE).
- This line DE intersects two sides of the triangle (AB and AC) at distinct points (D and E).
The converse states that:
- If the line DE divides two sides of the triangle proportionally (AD/DB = AE/EC), then the line DE is parallel to the third side (BC).
In simpler terms, if two segments cut across a triangle and divide opposite sides into equal ratios, those segments must be parallel to the third side.
It’s important to note that the converse is not the same as the original BPT. The converse needs the additional condition of proportional division to guarantee parallelism.
Here are some applications of the converse of BPT:
- Proving that the line joining the midpoints of two sides of a triangle is parallel to the third side (since the midpoint divides a side in half, creating a 1:1 ratio).
- Verifying if two lines are parallel by checking if they divide corresponding sides of two triangles proportionally.
Circle Theorem: Tangent Makes Right Angle With Radius

The tangent at any point of a circle is perpendicular to the radius drawn to the point of contact.
Here’s a breakdown of the concept:
- A tangent to a circle is a line that intersects the circle at exactly one point, called the point of contact.
- A radius is a line segment that connects the center of the circle to any point on the circumference.
The key property is that the radius drawn to the point of contact forms a right angle (90 degrees) with the tangent line passing through that point. There are a few ways to understand this:
- Intuitively: Imagine a line just grazing the circle. Since it only touches at one point, it creates a smooth transition, and a perpendicular line drawn from the center at that point would create the most direct path into the circle.
- Formally: Proofs exist that rely on properties of triangles formed by the radius, the tangent line, and a line drawn from the point of contact to another point on the circle. These proofs demonstrate that the angle between the radius and the tangent is always a right angle.
This property has various applications in solving problems involving circles, such as:
- Finding the length of a tangent from an external point
- Proving the relationship between tangents drawn from external points
- Constructing tangent lines to circles
Circle Theorem: Tangents Are Equal

That’s another important property of circles. The lengths of tangents drawn from an external point to a circle are indeed equal.
Here’s why:
- Imagine a circle with center O and an external point P.
- Draw two tangents (lines that touch the circle at one point only) from P to the circle, intersecting the circle at points Q and R.
Now, we can prove that PQ and PR (the lengths of the tangents) are equal:
- Since tangents are perpendicular to the radius drawn to the point of contact, we know angles POQ and POR are right angles (90 degrees).
- We also know that OP (the radius) is the same length for both triangles formed (triangle OPQ and triangle OPR) because it’s the distance from the center to a point on the circle (radius is constant).
- With these conditions, both triangles OPQ and OPR satisfy the Right-Hand Side (RHS) congruence criterion. This means that if two triangles have a right angle in the same location (corresponding angles) and a congruent side next to the right angles (radius), then the triangles are congruent.
- Because triangles OPQ and OPR are congruent by RHS, their corresponding sides (PQ and PR) must also be congruent. In simpler terms, PQ = PR.
Therefore, we have proven that the lengths of tangents drawn from an external point (P) to a circle are equal (PQ = PR).

Leave a Reply